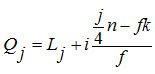Rumus-rumus dasar Statistika

. Ukuran Pemusatan Data

1. Rataan Hitung (Mean)

Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebutmean.

a) Rataan Hitung dari Data Tunggal 

b) Rataan Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi

Dengan : f_ix_i = frekuensi untuk nilai x_i yang bersesuaian

x_i = data ke-i

c) Rataan Hitung Gabungan

2. Modus

a. Data yang belum dikelompokkan

Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan m_o.

b. Data yang telah dikelompokkan

Modus dari data yang telah dikelompokkan dihitung dengan rumus:

Dengan : Mo = Modus

L = Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas

b₁ = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya

b2 = frekuensi kelas modus dikurangi frekuensi kelas intervalterdekat sesudahnya

3. Median (Nilai Tengah) 

a) Data yang belum dikelompokkan 

Untuk mencari median, data harus dikelompookan terlebih dahulu dari yang terkecil sampai yang terbesar. 

b) Data yang Dikelompokkan

Dengan : Q_j = Kuartil ke-j

j = 1, 2, 3

i = Interval kelas

L_j = Tepi bawah kelas Q_j

fk = Frekuensi kumulatif sebelum kelas Q_j

f = Frekuensi kelas Q_j

n = Banyak data

Simpangan Quartil (Q_d)

6. Simpangan baku ( S )

7. Simpangan rata – rata (S_R)

8. Ragam (R)

Contoh soal

Tabel 1.1 dibawah ini:

Jawab :

Read More

Download software "R" dari Pak Bayu

DOWNLOAD SEMUANYA

http://www.mediafire.com/?c44o6lvxs1nzsng
http://www.mediafire.com/?ucydco7t5slr4ml
http://www.mediafire.com/?gqcl906cist2ubi
http://www.mediafire.com/?jebdiztebtr0822
http://www.mediafire.com/?6aq42soceozhqc2
http://www.mediafire.com/?up6ck3uw6weub1c
http://www.mediafire.com/?bzd9bvv86x8898o
http://www.mediafire.com/?bzd9bvv86x8898o
http://www.mediafire.com/?1z39k9uk73fw3ut
http://www.mediafire.com/?s9exf3z08gbub1g
http://www.mediafire.com/?qzd61d34va8nzro

DOWNLOAD YANG INI, TERUS CUMA CLICK BAWAH INI AJA BUAT INSTALISASI
http://www.mediafire.com/?88tsl2v5639ib8b

Read More

download materi pak Bayu "Ke-2" versi "REVISI"

http://www.mediafire.com/?74cd1zpugd7xzbr

Read More

download materi pak Bayu "Statistika & Probabilitas" Pekerjaan Rumah

http://www.mediafire.com/?cpfwjpfdksguhpr

Read More

download XPS Viewer

http://www.mediafire.com/?6da3t13og4q4wfs

Read More

download materi UTS Bu Sofia "Revisi ke 2"

Sebelumnya kamu harus mendownload aplikasi XPS Viewer....


Kemudian kamu download filenya di :
http://www.mediafire.com/?pn2r5kxpsatex3k

Read More

Materi UTS Aplikasi Komputer "PRAKTIKUM" by Bu Sofia"Revisi 1"

http://www.mediafire.com/?q6sfcc93nd6h6u4

Read More

FUNGSI-FUNGSI PADA "MS.EXCEL"

http://www.mediafire.com/?o7aguidik2nfi9n

http://www.mediafire.com/?fx93grbz5nqn0yp

Read More

DOwnload Minitab 16

http://www.mediafire.com/?v4huydksyviqif4

Read More

Download MAteri Probabilitas & Statistika

http://www.mediafire.com/?kzb9wu8kq6aw49f

Read More

Pekerjaan Rumah "Ms. Excel" APLIKOM

http://www.mediafire.com/?v1lovlnc0y4efjv

Read More

Referensi Pascal

http://www.mediafire.com/?3uz24621r6ek61r

Read More

Download Referensi Probabilitas & Statistika " Click Here"

http://www.mediafire.com/?11wat2lpki4slax

http://www.mediafire.com/?3uz24621r6ek61r

Read More

Varian & Standar Deviasi

Varian dan Standar Deviasi

Salah seorang pembaca blog ini bertanya tentang maksud dari standar deviasi serta bagaimana mencari standar deviasi dari suatu kelompok data. Berangkat dari pertanyaan tersebutlah maka postingan tentang varian dan standar deviasi ini dibuat.

Berbicara tentang standar deviasi atau simpangan baku dalam bahasa Indonesia tidak bisa lepas dari varians. Hal ini karena standar deviasi adalah akar kuadrat dari varians atau sebaliknya, varians adalah kuadrat dari standar deviasi.

Salah satu ukuran variabilitas (measure of dispersion) yang paling sering digunakan jika data yang diukur berskala interval adalah varians. Varians didefinisikan sebagai rata-rata dari skor penyimpangan kuadrat. Untuk mencari varians, dibedakan antara varians populasi yang dilambangkan dengan (σ2) dengan varians sample yang dilambangkan dengan (s2).



Untuk varians populasi, dapat dicari dengan rumus:
Dimana:
µ = rata-rata populasi
N = total jumlah populasi
Adapun varians untuk sample dapat dicari dengan rumus yang sama namun mengurangkan N dengan 1 sebagai berikut:


Dimana :
s = rata-rata sample
n = jumlah sampel yang digunakan
untuk lebih memperjelas, baiklah kita coba dengan menghitung varians untuk populasi jika kita memiliki data pengukuran tentang nilai 5 siswa pada mata pelajaran matematika sebagai berikut:
7 7 9 8 6
Untuk menghitung varians dari data di atas maka kita harus mencari dahulu berapa mean (rata-rata) dari. Dengan rata-rata 6,9 maka kita tinggal memasukkan data di atas sebagai berikut:


Dengan varian sebesar 1,3 maka untuk mencari standar deviasi kita tinggal mengakar kuadratkan 1,3 yang akan menghasilkan 1,14. Karena varian adalah ukuran keberagaman data, maka semakin besar angkat varians maka semakin beragamlah data yang kita miliki dan semakin kecil nilai varians maka semakin homogenlah data yang kita miliki.
Nah, jika seandainya nilai varians yang kita miliki ternyata adalah 0, maka dapat disimpulkan bahwa dalam populasi atau sampel yang kita miliki tidak terdapat variabilitas. Keadaan demikian dapat terjadi jika sekor untuk setiap sampel/populasi adalah sama.

Selain rumus di atas, kita juga dapat menggunakan rumus-rumus lain untuk mencari varians. Pada dasarnya, pemilihan rumus yang digunakan tergantung pengguna yang merasakan rumus manakah yang paling mudah digunakan. Rumus-rumus yang lain tersebut diantaranya adalah:
Untuk varians sampel:

Read More

Probabilitas & Statistika ke-2

Macam-Macam Statistika :  

• Statistika Deskripsi

Menyajikan data dalam besaran-besaran statistik sehingga mudah diinterpretasikan seperti nilai minimum, rataan, simpangan baku, median, nilai maksimum atau menyajikan data-data dalam bentuk-bentuk diagram.

• Statistika Inferensi

Menggunakan statistika deskripsi untuk menaksir dan menguji besaran statistik.

• Data

Informasi yang dicatat dan dikumpulkan dalam bentuk asli, baik dalam bentuk hitungan maupun pengukuran.

• Percobaan statistik

Percobaan merupakan suatu proses yang berulangulang dan hasil proses itu tidak dapat diramalkan dengan pasti sebelumnya. Percobaan digunakan untuk menghasilkan data mentah.

Dasar-dasar teori peluang :

Ruang sampel

• Kumpulan dari semua hasil dari percobaan statistik, dinyatakan dengan notasi S

• Contoh : Percobaan pelemparan mata uang

Kejadian

• Dari setiap percobaan kita mungkin ingin mengetahui munculnya elemen-elemen dari ruang sampel yang mempunyai ciri tertentu. Sekelompok titik sampel itu membentuk himpunan bagian dari S

• Contoh : Percobaan pelemparan 3 koin

Operasi dengan kejadian

• Definisi 1 :

Irisan dua kejadian A dan B, dinyatakan dengan lambang A B ialah kejadian yang unsurnya termasuk A dan B.

• Contoh : Tentukan irisan antara A =

{1,2,3,4,5} dan B ={2,4,6,8}

Definisi 2

Dua kejadian A dan B saling terpisah bila A B = 0

• Contoh : Sebuah dadu dilantunkan. A menyatakan kejadian bahwa bilangan genap muncul di sebelah atas dan B kejadian bahwa bilangan ganjil yang muncul di sebelah atas.

Definisi 3

• Gabungan dua kejadian A dan B, dinyatakan dengan lambang A B ialah kejadian yang mengandung semua unsur yang termasuk A dan B atau keduanya.

• Contoh : Tentukan gabungan dari kejadian A = {1,2,3,4,5} dengan B = {2,4,6,8}

Definisi 4

• Komplemen suatu kejadian A terhadap S ialah himpunan semua unsur S yang tidak termasuk A. Komplemen A dinyatakan dengan lambang A'.

• Contoh : Q menyatakan kejadian bahwa seorang karyawan yang dipilih secara acak dari suatu pabrik adalah seorang perokok. Nyatakan kejadian komplemen Q ?

Read More

Program Utilitas

Program Utilitas yaitu Pemeliharaan Sistem "Maintance" & mengoperasikan sistem operasi.

E.g :

1. Search Utility
2. Image Viewer
3. Disk Clean-Up
4. Defragment Disk
5. Anti-Virus\
6. Spyware= Prog. yang mengumpulkan informasi secara diam-diam
7. Adware
8. Web-Filters
9. Anti spam-Programs
10. Pop UP-Blockers
11. Phishing Filters
12. A file Compression Utility (Menyusutkan File)
13. Media Player

Program Aplikasi :
     Applikasi Software, terdiri dari program-program membantu tugas-tigas pribadi.
Meliputi :

1. Business
2. Design Graphic
3. Personal/Education
4. Communacation

Applikasi Software (FORMAT) :

    Terdiri dari :

1. Pack. Software
2. Custom Software
3. Web Software
4. Open Source Software
5. Shareware
6. Freeware
7. Public Domain Software

Read More